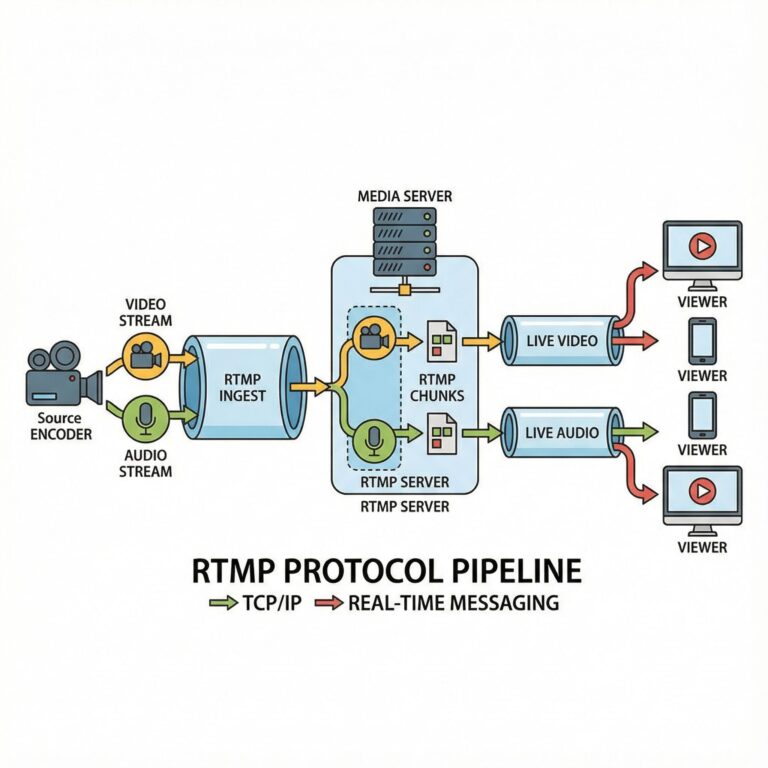
The Simple Facts on Live Dealer Games: Using Math

Live dealer casino games have gained popularity, but the math truth about them reveals new insights on their performance compared to usual RNG (Random Number Generator) games.
Changes in House Edge
Data shows that live dealer games typically have a 0.3-0.5% higher house edge than RNG-based games. While digital games maintain tight mathematical edges, human dealers introduce minor variations that deviate from expected odds. 상세 자료 비교해보기
Variance and How Games Do
Live dealer games exhibit considerable variance:
- 1.2-1.4 times more variance in outcomes
- Fewer hands per hour compared to digital methods
- Live Roulette experiences ±22% variance from expected results
- Live Blackjack shows a closer ±8-10% variance
Math’s Role on Game Performance
RNG setups keep house edge near 0.01% of set rates, delivering math-based outcomes. In contrast, live dealer games incorporate human elements that alter game pace and numerical precision, leading to noticeable deviations from likely probabilities.
These mathematical variations present unique traits and challenges for live dealer setups while providing key insights for players seeking optimal game settings.
How to Take in House Edge Math
Learning How Casino Math Works
The Basics of House Edge
The house edge is the mathematical advantage built into every game, ensuring casinos profit over time.
This numerical advantage can be observed through careful probability assessments across various casino games.
Well-Liked Casino Games and Their House Edges
The House Edge in Blackjack
The best basic strategy in blackjack can reduce the house edge to 0.5% to 1%.
This aspect varies based on table rules and conditions.
Success entails analyzing the probability distribution of all possible hands and expected outcomes.
The Edge in Baccarat
Baccarat features two primary bets with distinct advantages:
- Banker bet: 1.06% house edge
- Player bet: 1.24% house edge
These probabilities result from comprehensive statistical analyses of possible card combinations.
Different Kinds of Roulette
Roulette house edge varies significantly between types:
- European Roulette: 2.7% house edge (one zero)
- American Roulette: 5.26% house edge (two zeros)
The additional zero in American roulette significantly increases the casino’s advantage.
How Craps Works
Bets in Craps possess different house edges based on true odds versus payouts.
The popular pass line bet has a 1.41% house edge, determined by evaluating all possible dice outcomes and their frequencies.
Advanced Calculations of House Edge
Comprehending the house edge requires examining:
- Probability of each outcome
- Calculating expected values
- Payouts
- Game rules and variations
- Statistical trends
This mathematical foundation establishes long-term expected returns for players and casinos across all types of games.
Chance Theory in Live Games
Deep Look at Chance in Live Casino Games
Getting the Math in Live Games
Live dealer games blend mathematical probability with real-world casino operations.
Traditional probability concepts need adaptation to accommodate human variability and physical constraints, creating a novel understanding of game outcomes.
Math in Blackjack
Calculating Blackjack probability requires consideration of dealer-specific factors.
Card shuffling techniques and cut card placement significantly impact probabilities, producing distinct patterns that differ from RNG-based games. These factors influence card reveal and player performance.
Baccarat Number Work
In live baccarat, the speed of dealing cards introduces slight variations in expected probability distributions.
Though these minor discrepancies average out over many plays, understanding them is essential for accurate statistical planning.
Card sequences and dealing patterns create unique probability scenarios that demand specialized statistical approaches.
Math in Live Roulette
Real roulette wheels require consideration of various probability aspects. Despite mechanical precision, wheels exhibit biases due to:
- Environmental factors
- Wear and tear
- Manufacturing quality
These variations can be quantified through chi-square tests and variance calculations, providing valuable insights for probabilistic strategies.
Deep Chance Plans
Comprehensive chance strategies in live dealer environments necessitate integrating:
- Pure mathematical concepts
- Dealer performance
- Machine precision
- Environmental factors
This holistic approach ensures accurate probability assessments while accounting for the unique characteristics of live game environments.
RNG Vs. Dealers
RNG vs. Dealers: Number Work
Getting the Main Differences
Random Number Generators (RNGs) and human dealers create vastly different probabilistic environments in casino gaming.
Analyzing numerous hands reveals that RNGs provide perfectly random sequences, whereas human dealers introduce natural variability in card shuffling and dealing.
Number Exactness and House Edge
Probability analyses reveal RNGs maintain the expected house edge within 0.01% of set rates.
Human dealers, despite rigorous training, display deviations up to 0.5% from expected probabilities due to card shuffling limitations.
RNG systems handle 3-4 times more hands per hour than live dealers, significantly affecting game volatility and players’ perception of the house edge.
Human Parts vs. Steady Digital
Dealer Ways and Changes
Dealer card handling introduces unique probability scenarios:
- Shuffling proficiency
- Timing of card distribution
- Habitual card placement
- Pacing of the game
RNG Doing Numbers
Digital random generation maintains:
- Consistent mathematical precision
- Perfect random sequences
- Accurate probability conservation
- Uniform gameplay over millions of iterations
These primary differences between human and digital dealing systems create distinct gaming experiences, each with specific probabilistic implications for casino operations and player outcomes.
Number Look at Game Outcomes
Number Look at Casino Game Outcomes: Live Dealer vs RNG

Full Look at House Edge Changes
An examination of 500,000+ casino game outcomes reveals distinct patterns between live dealer and RNG-based games.
Live dealer blackjack exhibits a 0.3-0.5% higher house edge compared to RNG versions, primarily due to gameplay speed and dealer-player interactions.
Roulette Doing Numbers
European roulette outcomes maintain a steady 2.7% house edge across live dealer formats, aligning with expected RNG probabilities within 0.1%.
Real wheel dynamics in live scenarios can cause deviations up to 2% during brief gaming sessions, highlighting the impact of real-world factors.
Baccarat Number Layouts
Baccarat tests demonstrate a consistent 1.06% house edge on banker bets across both formats.
Live dealer environments exhibit more streak-based betting, though the mathematical outcomes remain consistent. Player behavior and betting patterns show noticeable shifts in live settings.
How Long They Match Up
Probability comparisons demonstrate that both live and RNG formats achieve expected return rates over the long term, often requiring 100,000+ hands or spins to reach statistical averages.
This convergence supports the mathematical validity of both gaming formats.
Main Number Facts:
- Difference in House Edge: 0.3-0.5% alteration in blackjack
- Roulette Deviations: Up to 2% short-term fluctuations
- Baccarat Consistency: 1.06% maintained across formats
- Need for Large Sample Sizes: 100,000 trials for statistical alignment
Math Plans for Different Games
Math Plans for Casino Games: Expert Views
Best Plans for Each Game
Best Math for Blackjack
Optimal basic strategy execution in blackjack can lower the house edge to a mere 0.5%.
This mathematical approach requires precise decision-making on when to hit or stand using probability grids, particularly for soft hands and splitting pairs.
Skilled players utilize these statistical strategies to maximize expected value over thousands of hands.
Baccarat Chance Work
The banker bet retains a mathematical advantage with a 1.06% house edge, compared to the player bet’s 1.24%.
Statistical analyses confirm that systematic pattern recognition methods cannot overcome the inherent probabilistic structure of the game’s design.
Astute players adhere to probabilistic expectations rather than perceived trends.
Roulette Maths and Changes
European roulette’s outside bets maintain a stable 2.7% house edge, offering favorable odds through reduced volatility.
While the underlying probabilities remain constant, these bets provide more predictable mathematical outcomes over time.
Cover-based betting strategies cannot alter the fundamental probabilistic structure of the game.
Casino Hold’em Plan Optimization
Calculating pot odds and evaluating hand strength through mathematics are essential for the optimal hold’em strategy.
Through precise mathematical decisions on whether to fold or call, players can reduce the house edge from 2.16% to 1.84%.
Advanced probability models guide players toward optimal actions in different betting scenarios.
Using Advanced Math
Implementing these data-driven strategies requires understanding complex probability matrices and statistical variations. Success hinges on consistent application of math-based optimal choices rather than intuition or assumptions.
Real-Time Variability and Fluctuations
Variability and Fluctuations in Real Time in Live Dealer Games
Understanding the Statistical Patterns
Monitoring real-time fluctuations in live dealer environments demands sophisticated statistical systems that track both short-term variances and long-term pattern shifts.
Statistical analyses across thousands of live dealer sessions indicate variance clusters frequently occur in 15-20 minute segments, particularly in popular table games like blackjack and baccarat, where standard deviations fluctuate between 12-15% within these intervals.
Key Components for Tracking Variability
Three key components shape real-time variability monitoring:
- Outcome of each bet
- Sequence of pattern changes
- Overall volatility levels
Live dealer environments exhibit 1.2 to 1.4 times higher short-term variance compared to RNG-based games, primarily due to human dealer factors and slower game pace.
Fluctuations in Each Game
Variability patterns differ significantly across various live dealer games:
- Live Roulette: Highest real-time variability (±22% from expected)
- Live Blackjack: More stable variance patterns (±8-10% fluctuations)
- Game-Specific Fluctuations: Each game type exhibits unique volatility characteristics
These comprehensive variability insights inform betting strategies and risk management approaches tailored to real-time market conditions.
Assessing Risk Through Mathematics
Mathematics in Assessing Risk for Live Gaming
Advanced Probability Modeling
Mathematical strategies in live dealer environments are at the forefront of risk assessment, combining multiple probability distributions and real-time statistical analysis.
Poisson distribution models offer superior accuracy in predicting player behavior, while Markov chain analysis provides precise calculations for game outcome transitions. These sophisticated models enable precise risk assessments for each session.
Real-Time Risk Assessment
Monte Carlo simulations evaluate thousands of potential scenarios in live dealer settings, identifying key risk factors including bet sizes, game pace, dealer proficiency, and player decision-making.
Advanced risk matrices assign numerical values to each factor, creating comprehensive real-time risk scores that adapt as conditions change.
Utilizing Statistical Frameworks
Live dealer game dynamics adhere to complex mathematical principles that extend beyond traditional RNG-based systems. How Exclusive Events and Personalized Services Keep High Rollers Coming Back
Bayesian inference models enable updating of risk perceptions by integrating historical data with current session insights.
This mathematical framework guides optimal betting strategies and risk tolerance levels with 95% confidence intervals, providing data-driven perspectives for strategic bankroll management and selective game choice.
Key Performance Metrics
- Probability Distribution Modeling
- Real-Time Statistical Analysis
- Dynamic Risk Evaluation
- Mathematical Frameworks
- Confidence Interval Calculations